Top Predicates Modes
French French German German ItalianItalian SpanishSpanish PortuguesePortuguese JapaneseJapanese KoreanKorean ChineseChinese

Data Types


So far, the only objects we have worked with have been what we have referred to as simply numbers. But in fact, FormulaOne programs can work with several different kinds of numbers, and there are other non-numeric objects they can manipulate, such as strings and lists of other objects. All these objects form the FormulaOne universe. Types, in FormulaOne, are just subsets of this universe. When we declare a variable to be of a certain type, we are saying that its value can come from that type's subset of the universe.
Here we should point out the distinction between objects and terms. A term is a FormulaOne expression, a purely linguistic sequence of symbols. An object is an abstract entity that some term refers to. For example, '22 + 3' and '25' are two different and distinct terms, but they both denote the same object, that is the number twenty-five.

Why Types?

Most conventional languages, such as Pascal and C, have some notion of the type of a variable. Some other languages, like LISP and some Prologs, have no such notion. Variables in these languages are just variables, and can take on any kind of value. Why does FormulaOne have types?
There are several reasons. Types make our programs more readable, because we can tell more easily what a variable represents. They also let us pass off to the compiler some of the work of checking arguments in predicate calls. And when the compiler knows what type a variable is, a program can represent it more compactly and access its value more efficiently.
Finally, giving types to variables allows FormulaOne to use decision procedures such as the one it uses for integer arithmetic. Languages which have no types, such as some dialects of Prolog, can't possibly do that because they can't distinguish between integers and any other kind of variable. These decision procedures involve the notion of constraint. Constraints are the pieces of information that FormulaOne places in the environment as it is computing the solution to a query. A constraint can be something as simple as the information that a variable has a certain fixed value, or the information that the sum of a group of variables is equal to another variable. We'll tell you what kinds of constraints can be put on each type of variable as we describe them.

Variable Declarations

As we have seen, variable declarations (such as x::L) can appear as formulas in queries or in the bodies of predicates, or as parameter declarations in predicate definitions. The most simple form of a variable declaration is the following:

var::type

In this template, var is a variable identifier. This can be any string of letters, numbers, and underscores, as long as it starts with a lower-case letter, and is not one of the FormulaOne reserved words. type is the name of a FormulaOne type, such as L, specifying what kind of variable it is. The four basic types in FormulaOne are L, I, R, and S. 
  x::L declares x to be a long integer
  x::I declares x to be an integer, having slightly different properties from the long ones
  x::R declares x to be a real number, that is, a number with a decimal part; and
  x::S declares x to be a string of characters.
We'll cover some other type expressions that can come after the "::" in due course, and even symbols that can go in place of the "::". At this point we will concentrate mainly on these four basic types.

Integers

I is the type of integers. Variables declared to be of this type are represented within the computer by the standard representation for integers (a block of 32 bits), which allows them to take on values from (-2,147,483,648 to 2,147,483,647). I variables can be compared to other I variables, and to integer constants (integers spelled out as sequences of digits). However, any constants which I variables are compared to must be in the above L range. The constraints that can be put on an I variable, say x, are of the format

x op n

or of the format

x op var + n

where op is one of the arithmetic relational operators ( = , <=, etc.), var is some other I variable, and n is some fixed integer value.
Whenever a formula with integers and a relational operator is processed by the query processor, it tries to put it into one of these forms by the laws of algebra. If it cannot, it will try to compute a value for some variable, if that is possible, or raise an exception ('Too many backtracks...') if it is not. So queries like 
all s::I & b::I & s = 40 & b = 3*s + 9
work with integers, because the value of s is known at the time the last formula is encountered.
All the previous queries will also work with I variables, up to the spiders and beetles example. But the query 
all s::I & b::I & s>0 & b>0 & 8*s + 6*b = 46
should give an exception, because FormulaOne cannot convert the last formula to the proper format for an I variable constraint.

Long Integers

L is the type of long integers of unlimited bit-precision.
The constraints that can be put on L variables are of the following form:

tlvl + t2v2 +....tnvn op m

where the ti's and m are long integer values, the vi's are long integer variables, and the op is an arithmetic relational operator (one of =, <, <=, <>, >, and >=).
In particular, the spiders-and-beetles formula 
8*s + 6*b = 46
is in this format already, and will be accepted as a long integer constraint. So as we have seen, the example from the last section will work if we have L variables instead of I. This gives L variables much more power than integers, quite apart from their wider range. However, FormulaOne will still not be able to solve some problems that humans can solve.
For example, consider the query 
all x::L & y::L & x > 0 & y > 0 & x * y = 46
This query is very similar to the spiders-and-beetles query, but it has one important difference: two variables, whose values are not known, are being multiplied together. Now we know that the pairs of possible values for x and y are 1 and 46, 2 and 23, 23 and 2, or 46 and 1. But FormulaOne does not know how to solve queries involving the multiplication of two unknown L variables, because it cannot convert it into a constraint of the proper form. An error condition would therefore be raised. One solution to this problem would be to put an upper bound on the value of one of the variables, by (for instance) changing the query to 
all x::L & y::L & x > 0 & y > 0 & y < 50 & x * y = 46
Then, FormulaOne could solve the equation by testing all values of y between 0 and 50 (not inclusive).
Your own knowledge and programming skills can be brought to bear on a problem. In this example, considerations of basic mathematics would lead you to an optimized query: 
all x::L & y::L & x > 0 & y > 0 & y < 24 & x * y = 46
FormulaOne will only test for y from 1 to 23 (obviously 24 or greater will not divide evenly into 46).
It might seem that you could optimize the query further by adding in y > x as another constraint. However when x is fixed then y is fixed as equal to 46/x so the additional constraint yields no benefit. You might wish that FormulaOne could solve problems like this in a better way. FormulaOne has taken the approach of being able to internally solve a very useful subset of possible queries, and that's a lot more than other logic or declarative languages do. A famous result of mathematical logic, Godel's Incompleteness Theorem, has as a consequence that there is no procedure or algorithmic problem-solver which will satisfy everybody. Nevertheless, your own problem solving method can be encapsulated into a predicate which will have the effect of acting as a constraint in the manner you desired. In any case, if you don't think you need the additional power or additional range of long integers in your problems, we would recommend that you use integers. They take up less memory in the computer, and because they can have fewer kinds of constraints on them, their decision procedure is more efficient.

Real Numbers

R is the type of real numbers. These are the numbers with fractional parts as well as integer parts. They are represented in memory by the conventional 64-bit representation of such numbers. Mathematically speaking, we can represent only rational numbers in this way, so these numbers might better be called rational (in both FormulaOne and other programming languages!). But in later versions of FormulaOne, R variables will stand for actual real numbers (roots of polynomial equations), and will have their own decision procedure, so we will call them reals.
Real-number constants are of the form 
[-]<digits>.<digits>
where <digits> is a sequence of one or more digits. (Note that there must be at least one digit before and after the decimal point.) For example, 232.45, -9999.0, 0.8937432, and 3.14 are all real constants, and can be compared to variables of type R.
Real-number constants can also be followed by an optional expression of the form 
e<digits>
or 
e-<digits>
indicating an exponent of 10 by which the constant will be multiplied. For instance, 2.17el0 represents the real number 21,700,000,000, and 314.15e-02 represents 3.1415.
A full decision procedure for real-number variables exists, but is very complex. The only constraints you can put on real variables in FormulaOne are of the format

x op n

or of the format

x op var + n

the same as for integers. Note, again, that this doesn't mean that you can't do arithmetic operations with real variables. You can do any addition, subtraction, multiplication, and division you want with them, as long as their values are known at the time the expression gets evaluated.

Strings

The type S is the type of character strings. This is the first non-numeric type we have encountered. A character string is just a sequence of characters, of any length. An S variable can have any string as value, regardless of length.
Constant terms of type S consist of the characters of the string, enclosed in single quotes. For example: 
'Maple Leaf'
'      $22.34  US'
' '
That last one is the null string, string containing no characters. If you want a string to contain the single quote character itself, you must represent it within the string by two single quotes. The string constant 
'The word ''word''.'
contains only the characters in the following line:
 The word 'word'.
You might now recognize that the Print formula is just a predefined predicate that can take strings as arguments: 
Print('wacka wacka')
Print('3.1415', 'nine')
Print('A   B C    ')
The term '\n', which you can print to cause Print to start a new line, is actually a string constant containing the carriage-return/line-feed (CR/LF) sequence. There are several other predefined predicates that work with strings. Len is a predicate with two arguments, the first of type S and the second of type I. A call to Len is true if and only if the length of the string is equal to the integer.
For instance, the query 
Len('Prolog', 6)
succeeds because the string 'Prolog' contains six characters; but the query 
Len('four', 7)
fails. Of course, Len can be used to find the length of a given string. The query 
all Len('$22.34 Cdn', length)
should give the single solution 'length = 10 '. The first argument to Len must have a value; x::S & Len(x, 5) will cause an error.
Append is a predicate which takes three string arguments, and succeeds if the third string is the concatenation of the first two. The first two arguments to Append, however, must have values, so it can really only be used to find the concatenation of two given strings. 
Append('foo','bar',str)
will result in str = 'foobar', while 
Append('foo ','bar', str)
will result in str = 'foo bar'.
Single characters can be extracted from strings by direct indexing. The first character has the index 0. The query 
all s = 'Vancouver' & s(3) = ch & ch = "c"
should succeed and give the solution ch = 99 for the variable ch. Characters are in FormulaOne represented by their Ascii codes taken as integers. The Ascii code for the character c is 99. The same integer is denoted by the character constant "c".
Here is a predicate which will allow us to take a string and pad it with periods (".") to 10 characters, if it is not that long. 
pred Dotpadded(string::S, outstring::S) iff
    {'string', padded to at least 10 characters, is 'outstring'}
    Len(string, x) & 
    (x >= 10 & outstring = string |
    x < 10 & Append(string, '.', newstring) & Dotpadded(newstring, outstring))
With these predicates declared, the following queries should all succeed: 
all Dotpadded('Chapter 9', 'Chapter 9.')
all Dotpadded('Andrews', 'Andrews...')
all Dotpadded('Srivallipurandan', 'Srivallipurandan')
x and newstring, it should be noted, can be used without a declaration because FormulaOne can tell from the context that they are supposed to be of type I and type S, respectively. When FormulaOne can do this, it declares the variables implicitly.

The Pairing Operation

The four basic types in the FormulaOne universe are integers and long integers, reals, and strings. But from those four basic types can be made many more data structures, by using the pairing operator, ",". When you place a comma in-between two terms, the whole thing forms a new term, the pair containing those terms. Some examples: 
(22,3)
('Dixie',0)
(x,(929.29,last))
As you can see, any two terms, be they integer, real or string, constant or variables, can be paired. The last example above even contains a pair as one element of a bigger pair. The comma operator, like an arithmetic operator, constructs a new term from two other terms on either side of it. The difference is that (22,3) is not equal to any other simpler term, whereas (22+3) is just another expression for 25. The type that every pair term belongs to is the type U, which we will encounter later. But they can also be used as constants of many other important types. The parentheses are not really necessary in the above examples; they are simply included for clarity. Pairing is right-associative, so the term 
(x, 929.29, last)
is equivalent to 
(x, (929.29, last))
and not to 
((x, 929.29), last)

The FormulaOne Universe

The complete set of objects - the things that terms can represent in FormulaOne - consists of all the real numbers, all the strings, and all possible pairs that can be made from applying the pairing operation to them any number of times. The long integers are a subset of the real numbers, and the integers are a subset of the long integers. This set of objects is called the universe of FormulaOne.

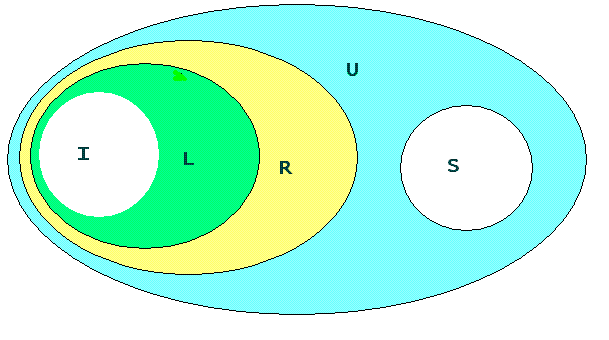
Every term we will encounter will refer to some object in this universe. Types are just subsets of this universe. The type consisting of the entire universe is called the universal type. U. R and S are basic types, but also subsets of the universal type; I and L are subsets of R, and so subsets of the universal type U too.
This means that when a term of one type is given as an argument to a parameter of another type (the situation usually referred to as a type clash in other languages), it doesn't necessarily cause a problem. Say we had the following predicate defined and compiled: 
pred Determ(a::R, b::R, c::R, det::R) iff
    det = ( (b*b) - (4*a*c) )
Then we could run the following query with no problems: 
all det x::R & x=2 & Determ(x, 3, 4, det)
even though the terms 2, 3, and 4 are integer constants, not real constants. Computationally, of course, FormulaOne has to convert the value of x from a 32-bit integer into a 64-bit real number, but it does so automatically because the value is logically a valid member of the type R.
The basic types of the universe are all referred to by name identifiers. But you can also use more complex type expressions to refer to many different useful types. The forms of type expressions have been chosen to represent the kinds of types that programmers frequently want.

Subranges

Recall our original spiders-and-beetles query. Since we can guess that there must be between 1 and 10 of both spiders and beetles, we could have phrased that query in the following way: 
all s::[1..10] & b::[1..10] & 8*s + 6*b = 46
We could read this, in English, as "s and b are between 1 and 10, and 8*s + 6*y is equal to 46." It is equivalent to saying 
all s::I & s>=0 & s<=10 & b::I & b>=0 & b<=10 & 8*s + 6*b = 46
Expressions of the form

[n..m]

for any numbers n and m, stand for the type containing all the integers from n to m. They act just like the type names I, S, and so on, and can be used in parameter and local variable declarations just like them. Some examples: 
ftemp::[-32..212] 
delta:[-1..1] 
son:[1..7]
These type expressions are called subranges, and will become particularly important when we talk about arrays. But even here, they have the effect of making the program code more compact and readable, which is always a benefit. Normally the variables declared as being of subrange types are represented as I variables, with the associated capabilities and constraints. If you want them to be represented as L variables, with their more powerful constraints, you can use the form

L[n..m];

for example 
ftemp::L[-32..212]

Lists

We can declare a variable, say x, as being a list of integers by the declaration x::list I. This declaration has a precise technical meaning in FormulaOne. All the following terms are constants of type list I and can therefore be compared to x: 
(1, 1, 2, 3, 5, 8, Nil)
Nil
(32767, Nil)
The set of all objects of type list I can be defined recursively as follows:
Nil stands for the list with no elements. It is an empty list which cannot be represented by a pair (head,tail). Every list must be terminated with the term Nil (this also allows the compiler to distinguish a list from a pair). Nil is really just another term representing the object 0 in the universe; but FormulaOne will not let you give the term 0, or any arithmetic expression equivalent to it, as a list. It allows only the term Nil itself.
We can use lists of other types too, for instance list L, list S, and list [-32..212]. Here is a predicate that may come in handy for processing lists of long integers. 
{Line 1} pred Sum(l::list L, sum::L) iff
{Line 2}    {The sum of the list 'l' is 'sum'}
{Line 3}    l = Nil &
{Line 4}    sum = 0
{Line 5}    | l = (head, tail) &
{Line 6}    Sum(tail, tailsum) &
{Line 7}    sum = head + tailsum
Sum is a recursive predicate (i.e. one which calls itself, that is, self-referential). If the list is Nil, the sum computed is 0; otherwise, the list is broken into a head and tail.
The formula l = (head,tail) is a deconstructor of a list. This deconstructor decomposes l for your convenience (but does not destroy it) and in the process implicitly defines two new variables which we will call head and tail: 
head::L tail::list L
For example, if l = (3,44,Nil) then head = 3 and tail = (44,Nil). Another implicit definition of a symbolic variable occurs in line 6.: 
Sum(tail,tailsum)
tailsum is implicitly defined as a symbolic variable of type L, in agreement with the definition of the variable sum in line 1.
The predicate Sum, simple as it is, illustrates important concepts and so it is worthwhile to go through it with an example.
In computing the query all Sum ((3,44,Nil),x), lines 3 and 4 have no effect because l = (3,44,Nil) and so l <> Nil (i.e. l is not equal to Nil). Line 5 deconstructs l into a head of 3 and a tail of (44,Nil). Line 6 recursively calls Sum with new arguments tail and tailsum.

We go back to line 1 and replace l by tail and sum by tailsum. Note that sum and tailsum have not yet received any value. Again, lines 3 and 4 have no effect but line 5 deconstructs l into head = 44 and tail = Nil.

The next recursive call in line 6 in Sum(Nil, tailsum). This is a new tailsum but the compiler is aware of that and keeps track of the versions of tailsum. In this call lines 3 and 4 are finally executed and this time tailsum gets a value, which is 0.

Control passes "back up one level" and line 7 is executed: sum = 44 + 0 = 44.

Next control passes up to the first recursive call where head was 3 and line 7 executes and gives a final sum = 3 + 44 = 47.

There are other and better ways to achieve what Sum accomplishes, but you should have a clear idea of its mechanism because Sum incorporates critical ideas about lists, recursion and declarative programming in general.
Lists are recursive data structures, so recursive predicates fit them well. You will frequently encounter recursive predicates, and the need for them, when you work with lists. There are several predefined predicates for lists. Len and Append, which we encountered for strings, also work with any kind of list type as well as strings. (They are, technically, polymorphic predicates - they can take many types of terms as arguments.) Len gives the number of elements in the list, and Append makes a list out of the elements of the first list, followed by the elements of the second.

There is also a list membership operator, in, which you can use to test or assert that a term is in a given list. The following query should succeed: 
all x::I & z::list I & x = 2 & z = (3, 2, Nil) & x in z
the test x in z succeeds since 2 is a term of z. The similar query 
all x::I & z::list I & z = (3, 2, Nil) & x in z
should give you two solutions, one with x = 3 and the other with x = 2.

Summary


Top Predicates Modes